How tan(π/4-θ) = (1−tanθ)/(1+tanθ) ?
Derivation of
tan(π/4-θ) = (1−tanθ)/(1+tanθ)
As, tan(π/4+θ) = (1+tanθ)/(1-tanθ)
...........👉👉Derivation of tan(π/4+θ) = (1+tanθ)/(1-tanθ)
{Put θ= -θ}
tan(π/4-θ) =
[1 + tan(-θ)] /[1- tan(-θ)]
{ As tan(-θ) = -tanθ }
Hence,
tan(π/4-θ) = (1-tanθ)/(1+tanθ)
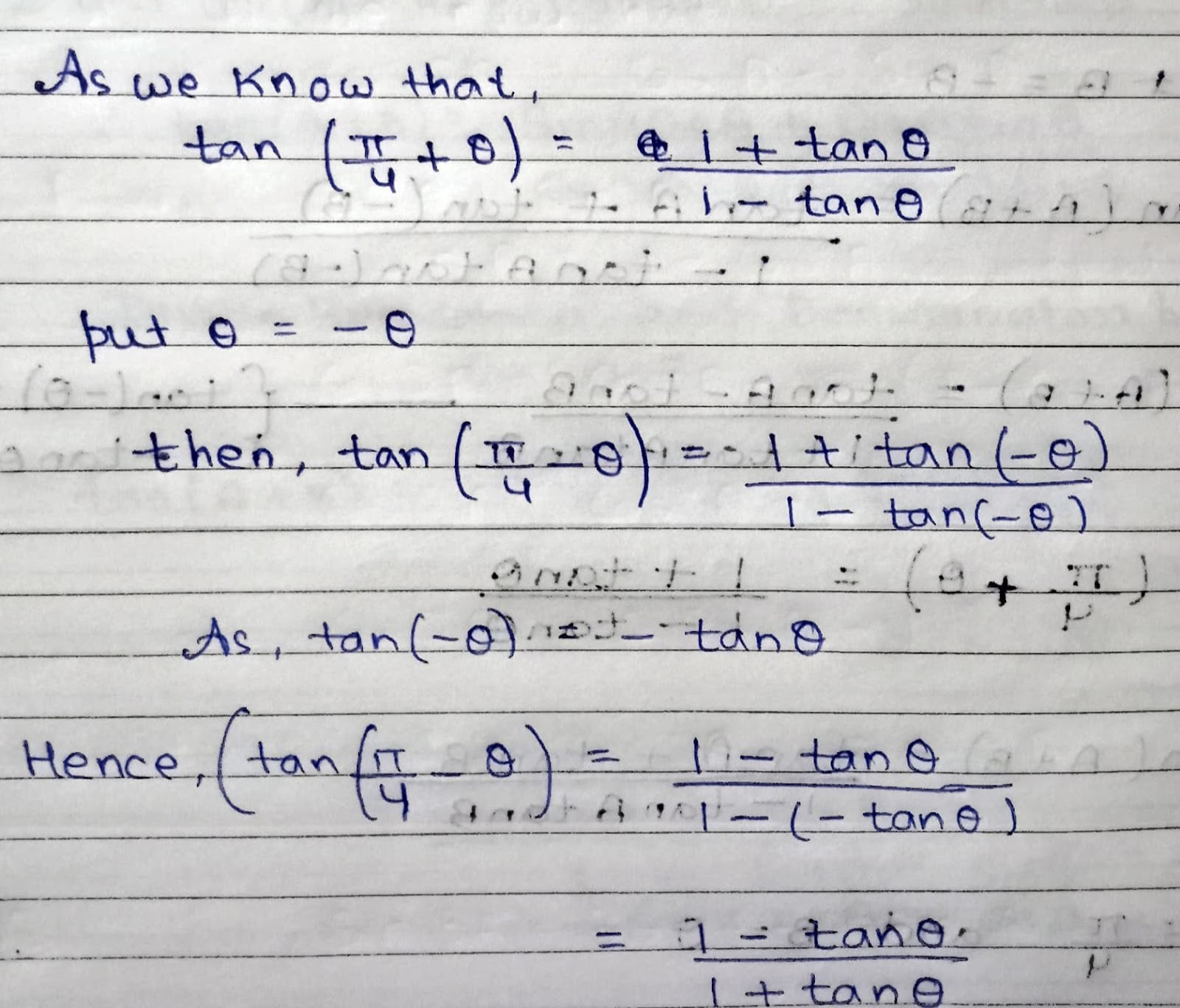



Comments
Post a Comment
Comment here