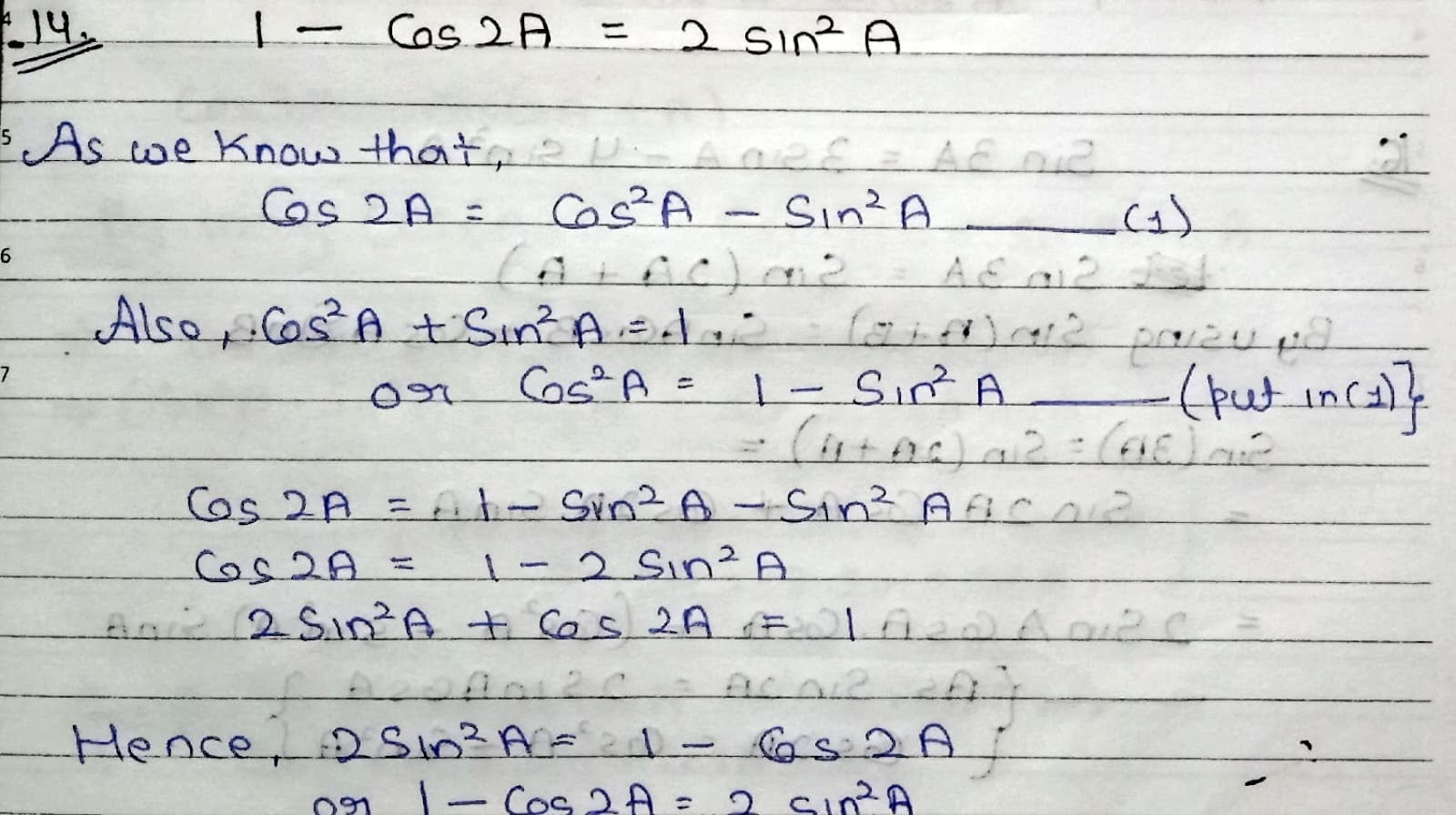ANAND KUMAR UPADHAYAY

How Cos 2θ = (1 - tan²θ)/ (1 + tan²θ) ? ➡ Cos(2A) = Cos²A - Sin²A

How Sin 2θ = (2 tanθ)/(1+ tan²θ) ? ➡ Sin(2A) = 2 SinA CosA

How tan (3A) = (3tanA - tan³A)/(1-3tan²A)? 👉 How tan(A+B) = (tanA + tanB)/(1- tanA tanB ) ?

How tan (2A) = (2 tan A)/ 1- tan²A? ➡   How tan(A+B) = (tanA + tanB)/(1- tanA tanB ) ?

Cos (3A) = 4 Cos³A - 3 CosA?

How sin 3A = 3SinA - 4Sin³A? Sin(3A) = Sin(2A +A) As we know that Sin(A+B) = SinA CosB + CosA SinB then,  ➡Sin(2A + A) = Sin2A CosA + Cos2A SinA also, { Sin(2A) = 2 SinA CosA } .........(1) { Cos(2A) = Cos²A - Sin²A } ......(2) Put the value of (1) and (2) in formula ➡Sin(2A + A) = (2 SinA CosA)CosA + (Cos²A - Sin²A)SinA also,  Cos²A = 1 - Sin²A ➡Sin(2A + A) = 2 SinA Cos²A + (Cos²A - Sin²A)SinA ➡Sin(2A + A) = 2 SinA (1- Sin²A) + (1- Sin²A -Sin²A) SinA ➡Sin(2A + A) = 2 SinA (1- Sin²A) + (1- 2Sin²A) SinA ➡Sin(2A + A)= 2 SinA - 2Sin³A + SinA - 2Sin³A ➡ Hence, Sin(2A + A)= 3SinA - 4Sin³A

How Cos (2A) = 2 Cos²A - 1 ? As we know that  ➡  Cos(2A) = Cos²A - Sin²A .......(1) Also Sin²A + Cos²A = 1  or Sin²A = 1 - Cos²A......[put in (1) eq.] ➡Cos (2A) = Cos²A - (1 - Cos²A)                 = Cos²A - 1 + Cos²A Hence,            Cos (2A) = 2 Cos²A - 1          or 1 + Cos(2A) = 2 Cos²A ➡ If angle is half i.e. θ = A then, Cos (A) = 2 Cos²(A/2) - 1       or 1 + Cos(A) = 2 Cos²(A/2)

How 1 - Cos2A = 2 sin²A? As we know that, Cos(2A) = Cos²A - Sin²A.........(1) ........👉{ Cos(2A) = Cos²A - Sin²A } also, Sin²A + Cos²A = 1       or Cos²A = 1- Sin²A......(2) ...............👉{ How Sin²θ + Cos²θ = 1?? } put eq. (2) into eq.(1) Cos(2A) = 1 - Sin²A - Sin²A Hence, Cos(2A) = 1 - Sin²A also, 1 - Cos2A = 2 sin²A  If angle(ϴ) is halved, then, CosA = 1 - Sin²(A/2) or  1 - CosA = 2 sin²(A/2)

Derivation of  Cos(2A) = Cos²A - Sin²A or Cos(A) = Cos²(A/2) - Sin²(A/2) ? As we know that, Cos(A+B) = CosA CosB - SinA SinB ........👉👉{ Cos(A+B) = CosA CosB - SinA SinB } put B= A  we get, ⇒Cos(A+A) = CosA CosA - SinA SinA ⇒Hence, Cos(2A) = Cos²A - Sin²A ⇒If angle will be halved i.e. θ = A Then,      ⇒ Cos(A) = Cos²(A/2) - Sin²(A/2)

Derivation of   Sin(2A) = 2 SinA CosA or Sin(A) = 2Sin(A/2) Cos(A/2)? As we know that, ⇒Sin(A+B) = SinA CosB + CosA SinB 👉👉( Sin(A+B) = SinA CosB + CosA SinB ) put B= A then, ⇒Sin(A+A) = SinA CosA + CosA SinA    ⇒Sin(2A) = SinA CosA + SinA CosA Hence, Sin(2A) = 2SinA CosA ⇒If angle will be halfed i.e. θ = A ⇒Hence,        Sin(A) = 2Sin(A/2) Cos(A/2)

Derivation of tan(π/4-θ) = (1−tanθ)/(1+tanθ) As, tan(π/4+θ) = (1+tanθ)/(1-tanθ) ...........👉👉 Derivation of tan(π/4+θ) = (1+tanθ)/(1-tanθ) {Put θ= -θ} tan(π/4-θ) = [1 + tan(-θ)] /[1- tan(-θ)]         { As tan(-θ) = -tanθ } Hence, tan(π/4-θ) = (1-tanθ)/(1+tanθ)

Derivation of tan(π/4+θ) = (1+tanθ)/(1-tanθ) As,  tan(A+B) = (tanA - tanB)/(1- tanA tanB)        👉 Derivation of tan(A+B) = (tanA + tanB)/(1- tanA tanB) { Put A = π/4 and B= θ } tan(π/4+θ) = [tan(π/4) + tanθ] /[1- tan(π/4)tanθ] As tan(π/4) = 1.......(i.e. tan 45° = 1) Hence,  tan(π/4+θ)= (1+tanθ)/(1-tanθ)

Derivation of tan(A-B) = (tanA - tanB)/(1+ tanA tanB) 👉👉 Derivation of tan(A+B) = (tanA + tanB)/(1- tanA tanB) 👉👉 Derivation of Sin(A+B) = SinA CosB + CosA SinB 👉👉 Derivation of Cos(A+B) = CosA CosB - SinA SinB

Derivation of tan(A+B) = (tanA + tanB)/(1- tanA tanB )  👉👉 Derivation of Sin(A+B) = SinA CosB + CosA SinB 👉👉 Derivation of Cos(A+B) = CosA CosB - SinA SinB

👉 These are the values of trigonometric Ratios:- 👆 Picture showing values of sinθ,cosθ,tanθ where θ is the some angle. From the table values of Cosecant (Cosec), Secant(sec) and Cotangent (Cot) can be determined. As,  Cosecθ = 1/Sinθ         Secθ = 1/cosθ and  Cotθ = 1/tanθ or cosθ/sinθ 👉 What is Trigonometry? 👉 What is a right angled triangle?

Trigonometric Ratios :- There are only six possible ratios of sides of a right angled triangle. In Trigonometry, different names are given to those ratios of right angled triangle w.r.t. angle ∠θ These are the ratios:- {1}. P/H :-  Sine (sin) {2}. B/H :- Cosine (Cos) {3}. P/B :- tangent (tan) {4}. H/P :- Cosecant (cosec) {5}. H/B :- Secant (Sec) {6}. B/P :- Cotangent (Cot) where P :- Perpendicular B:- Base H:- Hypotenuse source:  Wikipedia Some simple identities : ⇒tanϴ = 1/ cotϴ or sinϴ/ cosϴ ⇒Cosecϴ = 1/ sinϴ ⇒Secϴ  = 1/ cosϴ ⇒Cotϴ = 1 / tanϴ or cosϴ/ sinϴ 👉👉 What is Trigonometry? 👉👉 Trigonometry Table (Values of Trigonometric ratios) 👉👉 How Sin²θ + Cos²θ = 1?

What is Trigonometry? Trigonometry is a branch of mathematics that studies relationships between side lengths and angles of triangles. 👉👉 What is a Right angled triangle?

Derivation of Cos(A-B) = CosA CosB + SinA SinB 👉👉 Derivation of Cos(A+B) = CosA CosB - SinA SinB

Derivation of Cos(A+B) = CosA CosB - SinA SinB

How Sin(A-B) = SinA CosB- CosA SinB 👉👉( Derivation of Sin(A+B) = SinA CosB + CosA SinB )

Derivation of Sin(A+B) = SinA CosB + CosA SinB

Derivation of 1 + cot²θ = cosec²θ As we know that, Sin²θ + Cos²θ = 1........👉👉( Derivation of Sin²θ + Cos²θ = 1 )   Divide by sin²θ both sides , we get   Sin²θ/sin²θ + Cos²θ/sin²θ = 1/sin²θ {1/sin²θ = cosec²θ  and Cos²θ/sin²θ= Cot²}   Hence,       1 + cot²θ = cosec²θ

Derivation of tan²θ + 1 = sec²θ As we know that,               Sin²θ + Cos²θ = 1  ........👉👉( Derivation of Sin²θ + Cos²θ = 1 ) Divide by Cos²θ both sides ,    we get, Sin²θ/Cos²θ + Cos²θ/Cos²θ = 1/Cos²θ Hence,    tan²θ + 1 = sec²θ

How   Sin²θ + Cos²θ = 1...?? According to Pythagoras theorem, "the square of hypotenuse(H) is equal to the sum of square of base(B) and perpendicular(P)" i.e.     H² = B² + P² (Dividing both sides by H²) we get,     H²/H² = B²/H² + P²/H²        1   = Sin²θ + Cos²θ                       ....(B/H  = sinθ and P/H = cosθ) Hence, Sin²θ + Cos²θ = 1 How Sin²θ + Cos²θ = 1?

Right angled triangle :   Right angled triangle is a triangle in which one angle is a right angle (that is, a 90-degree angle). # The relation between the sides and angles of the right angled is the basis for trigonometry. # Pythagoras Theorem states that The square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of other two sides. 

👉Important Rules for trigonometric values in 1st ,2nd ,3rd and 4th Quadrant. {1}.    Quadrant 1st: (90°-θ) and (360°+θ) All Trigonometric values are Positive (+). {2}. Quadrant 2nd :  (90°+θ) and (180°-θ) Only values of sine (sin) and Cosecant (cosec) is positive (+) rest all Trigonometric values are negative (-). {3}. Quadrant 3rd:  (180°+θ) and (270°-θ) Only values of tangent (tan) and Cotangent (cot) is positive (+) rest all Trigonometric values are negative (-). {4} . Quadrant 4th :  (270°+θ) and (360° -θ) Only values of cosine (cos) and Secant (sec) is positive (+) rest all Trigonometric values are negative (-). 👇 The picture showing the values of all Trigonometric ratios in different quadrants :- # A Simple Way to remember A DD : All values positive S UGAR : Sine,Cosine are positive T O : Tan, cot are positive C OFEE : cos ,sec are positive