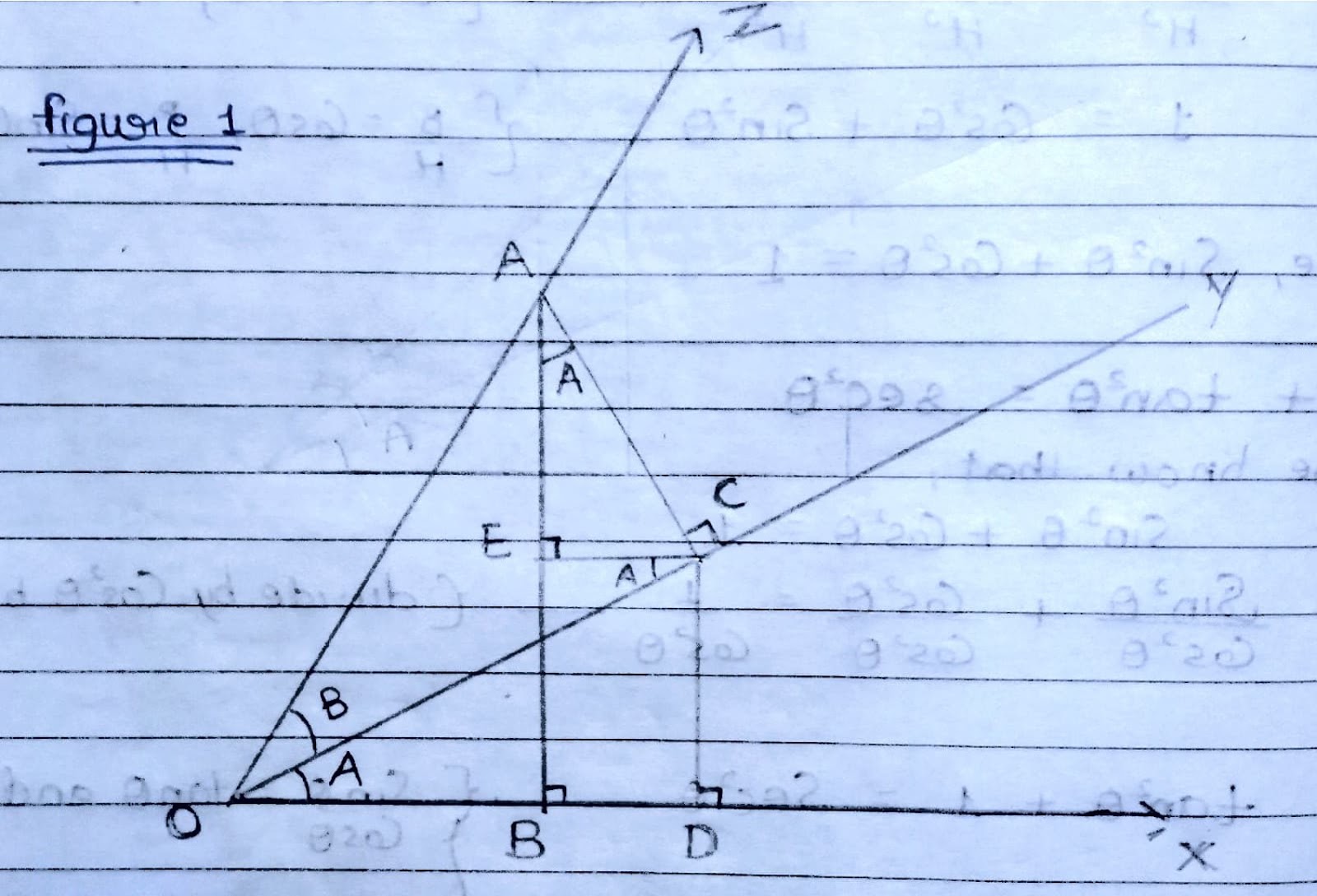
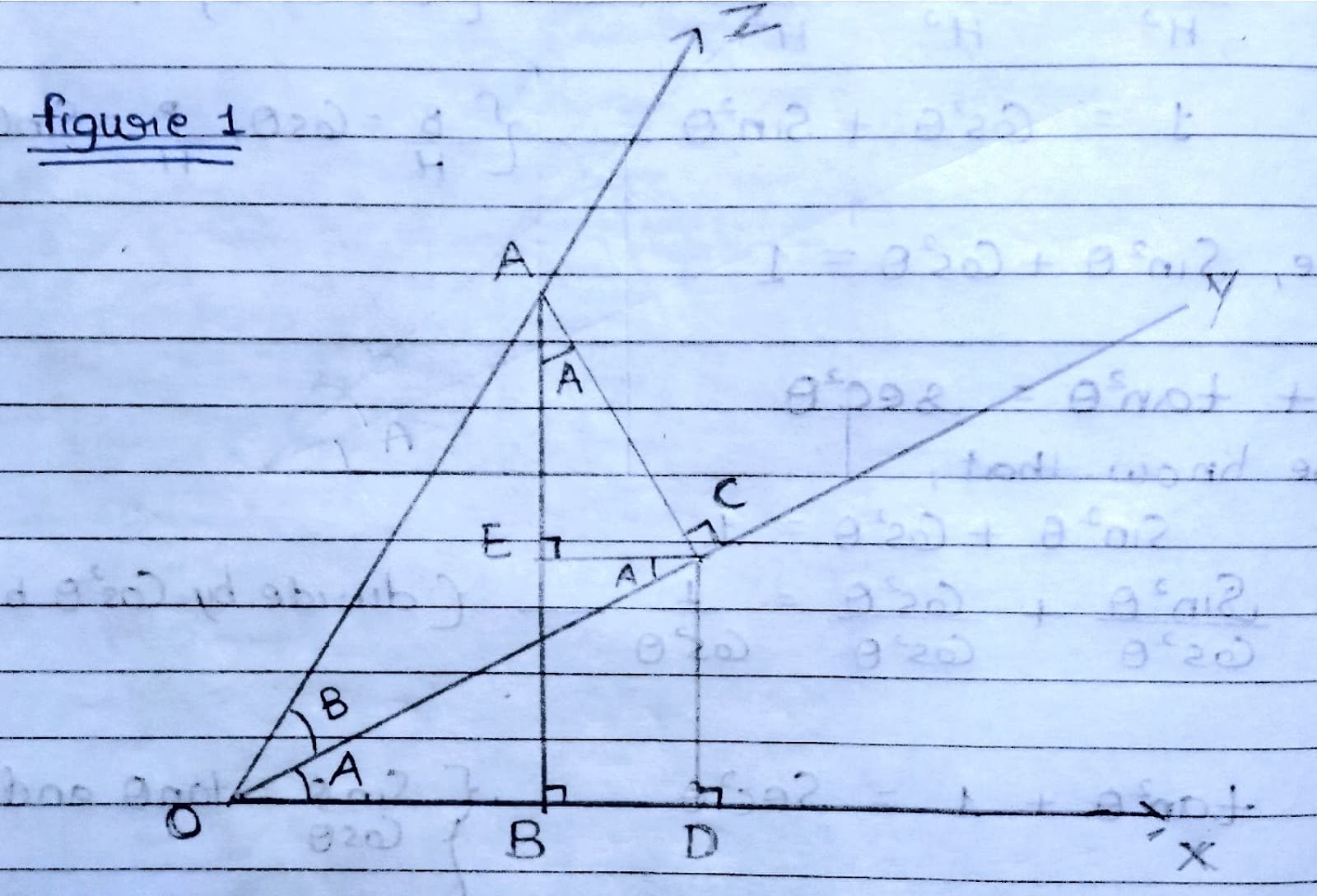
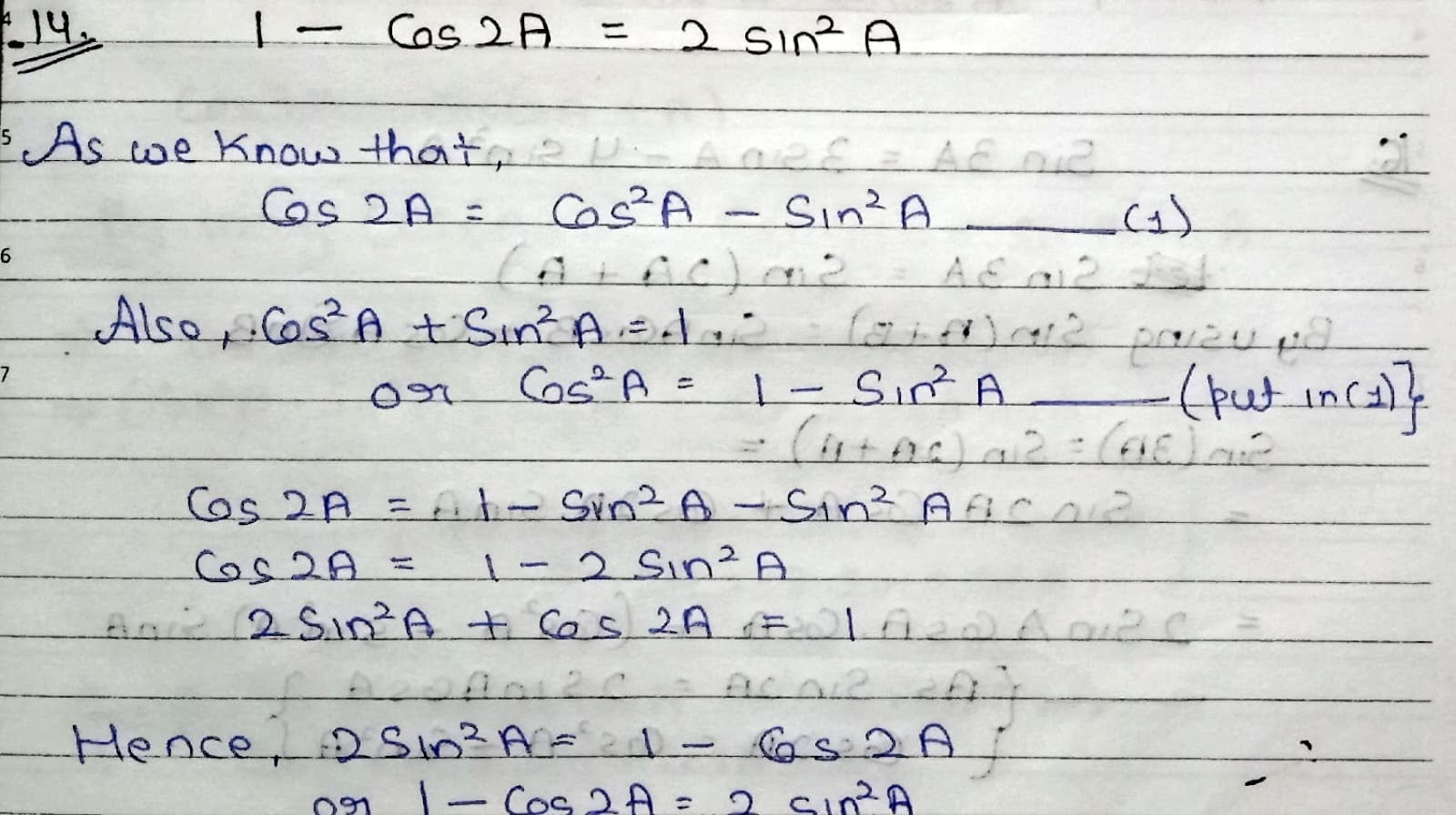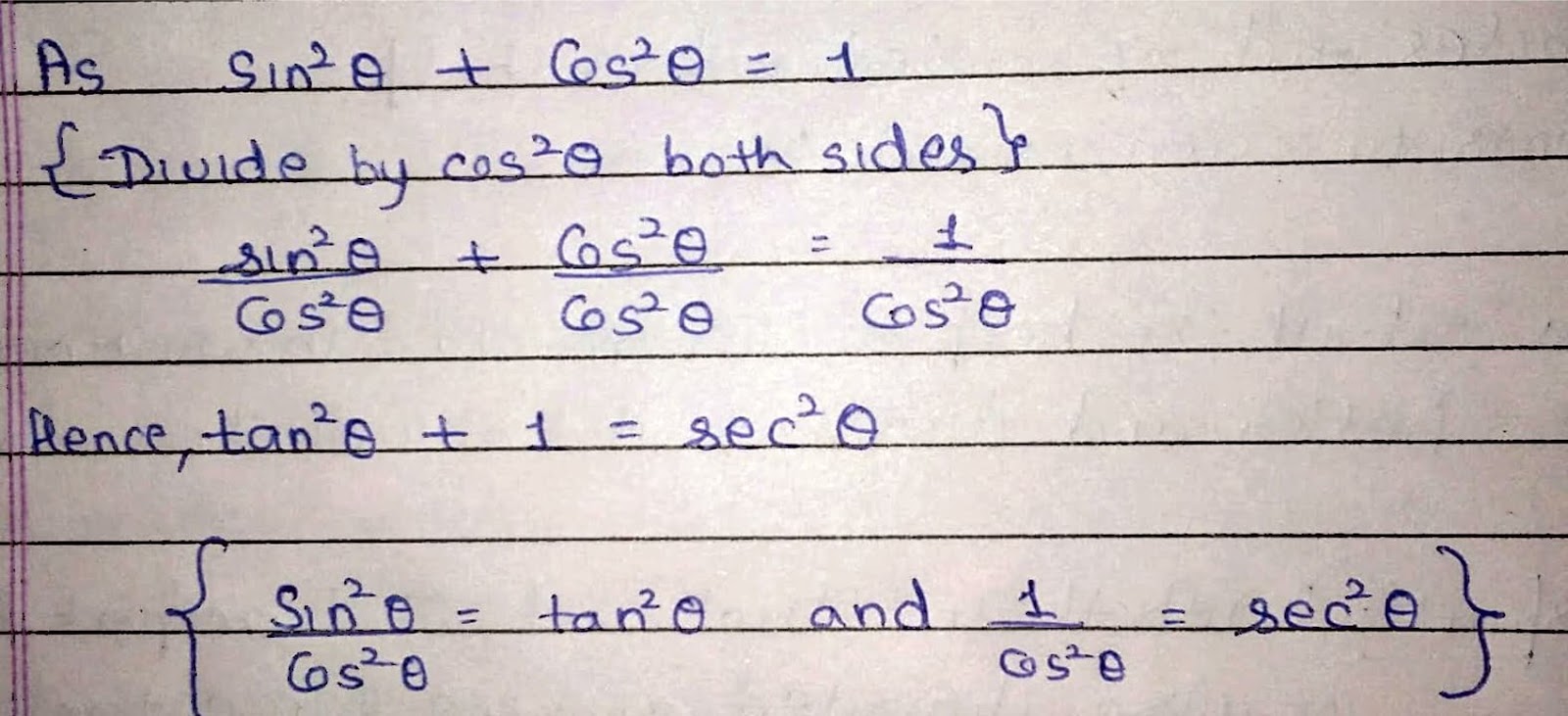How 1 + Cos (2A) = 2 Cos²A ?
How Cos (2A) = 2 Cos²A - 1 ? As we know that ➡ Cos(2A) = Cos²A - Sin²A .......(1) Also Sin²A + Cos²A = 1 or Sin²A = 1 - Cos²A......[put in (1) eq.] ➡Cos (2A) = Cos²A - (1 - Cos²A) = Cos²A - 1 + Cos²A Hence, Cos (2A) = 2 Cos²A - 1 or 1 + Cos(2A) = 2 Cos²A ➡ If angle is half i.e. θ = A then, Cos (A) = 2 Cos²(A/2) - 1 or 1 + Cos(A) = 2 Cos²(A/2)